| 09 August 2024 | Challenge 281 |
Colors of the Knight
Task 1: Check Color
Submitted by: Mohammad Sajid Anwar
You are given coordinates, a string that represents the coordinates of a square of the chessboard as shown below:
Write a script to return true if the square is light, and false if the square is dark.
Example 1
Input: $coordinates = "d3"
Output: true
Example 2
Input: $coordinates = "g5"
Output: false
Example 3
Input: $coordinates = "e6"
Output: true
Solution
We split the square’s coordinates into column and row, convert these to zero-based indices and take the Manhattan distance from a1 modulo 2.
All squares having an odd distance are light.
use strict;
use warnings;
sub check_color {
my ($col, $row) = shift =~ /^([a-h])([1-8])$/ or die "field invalid";
(ord($col) - ord('a') + $row - 1) % 2;
}
See the full solution to task 1.
Task 2: Knight’s Move
Submitted by: Peter Campbell Smith
A Knight in chess can move from its current position to any square two rows or columns plus one column or row away. So in the diagram below, if it starts a S, it can move to any of the squares marked E.
Write a script which takes a starting position and an ending position and calculates the least number of moves required.
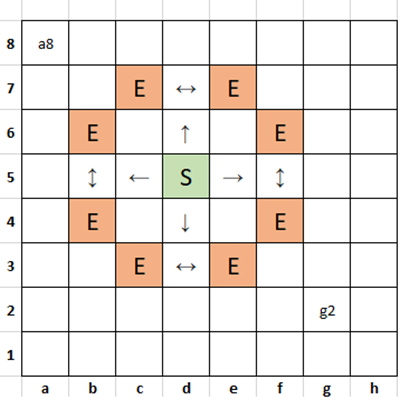
Example 1
Input: $start = 'g2', $end = 'a8'
Ouput: 4
g2 -> e3 -> d5 -> c7 -> a8
Example 2
Input: $start = 'g2', $end = 'h2'
Ouput: 3
g2 -> e3 -> f1 -> h2
Solution
Theory
In mathematics, a graph \(G = (V, E)\) consists of a set \(V\) of vertices and a set \(E\) of edges, where an edge connects two nodes.
There are several ways to represent a graph.
One representation that suites this task is in the form of an adjacency matrix.
The adjacency matrix is indexed by the vertices as rows and columns and contains a one for vertices that are directly connected by an edge and a zero otherwise.
The powers \(A^n\) of the adjacency matrix have an interesting property: The element \(a_{ik}^{(n)}\) contains the number of walks between the vertices \(i\) and \(k\) having a length of exactly \(n\).
Therefore the smallest power \(A^n\) of \(A\) where \(a_{ik}^{(n)}\) is nonzero gives the shortest path between \(i\) and \(k\).
For this task we take the chessboard’s squares as vertices and connect those vertices with an edge, where a knight is allowed to move between the respective squares.
As the setup is symmetric in both axes, we may exchange rows and columns, the direction of the axes and even start and end.
Practice
The only difficulty with the above theoretical approach is the construction of the actual adjacency matrix. As our vertices are already elements of an 8x8 matrix, the adjacency matrix can be seen as a four dimensional, 8x8x8x8-sized hypermatrix. However, to calculate the powers of our adjacency matrix, we need to revert this view and multiply true matrices with a size of 64x64.
Using PDL it is easy to look at the adjacency matrix either as an 8x8x8x8 or as a 64x64 ndarray.
Looking at the adjacency matrix as a 4-d ndarray we may fix a starting vertex and retrieve a matrix that specifies all corresponding end vertices. Thus we may regard this hypermatrix as a stack of boards, each of which has its own unique starting vertex.
Picking one of these boards, we may view at the neighborhood of the starting vertex and apply the matrix of possible knight’s moves on this neighborhood. Note that a neighborhood matrix may legally extend beyond the board.
To construct such a series of sub-ndarrays, PDL comes with the very powerful range method.
As the neighborhood matrices and the original ndarray are connected via dataflow, modifications in the submatrices will result in modifications in the original ndarray.
The adjacency matrix is constant for this task and thus may be constructed beforehand. Its powers will be cached.
use strict;
use warnings;
use PDL;
use PDL::NiceSlice;
use experimental 'signatures';
use constant N => 8;
BEGIN {
my $moves = long [0, 1, 0, 1, 0],
[1, 0, 0, 0, 1],
[0, 0, 0, 0, 0],
[1, 0, 0, 0, 1],
[0, 1, 0, 1, 0];
my $adj = zeros long, N, N, N**2;
$adj->range(identity(N**2)->splitdim(0, N)->whichND - indx(2, 2, 0),
[5, 5], 't')->reorder(1, 2, 0) .= $moves;
$adj = $adj->clump(0, 1);
memoize 'adj', SCALAR_CACHE => 'MERGE';
sub adj ($n) {
return identity(N**2) unless $n;
die "not implemented" if $n < 0;
adj($n - 1) x $adj;
}
}
sub knights_move {
my @fields = map ord() - ord(/\d/ ? '1' : 'a'),
map /^([a-h])([1-8])$/, @_;
die "start and end fields required" unless @fields == 4;
adj($_)->splitdim(1, N)->splitdim(0, N)->(@fields) &&
return $_ for 0 .. N**2 - 1;
'inf';
}
Once we have constructed our adjacency matrix, we may extend the task and ask for the diameter of a chessboard, measured in knight’s moves, i.e. what is the maximum over the minimum number of knight’s moves between any two squares on the board.
Here we need to sum over all powers of the adjacency matrix until there are no zero elements left.
sub diameter {
my $walks = zeroes adj(0);
for (0 .. N**2 - 1) {
$walks += adj($_);
return $_ if all $walks;
}
'inf';
}
The answer is six.
With a little more playing we may find the most distant pairs:
sub not_within ($n) {
my $walks = zeros adj(0);
$walks += adj($_) for 0 .. $n;
whichND !$walks->splitdim(1, N)->splitdim(0, N);
}
not_within(5) produces
[
[7 7 0 0]
[0 7 7 0]
[7 0 0 7]
[0 0 7 7]
]
i.e. the path length of six occurs only between diagonally opposite corners.
See the full solution to task 2.
If you have a question about this post or if you like to comment on it, feel free to open an issue in my github repository.