| 19 December 2025 | Challenge 352 |
Triangular Squares
Task 1: Match String
Submitted by: Mohammad Sajid Anwar
You are given an array of strings.
Write a script to return all strings that are a substring of another word in the given array in the order they occur.
Example 1
Input: @words = ("cat", "cats", "dog", "dogcat", "dogcat", "rat", "ratcatdogcat")
Output: ("cat", "dog", "dogcat", "rat")
Example 2
Input: @words = ("hello", "hell", "world", "wor", "ellow", "elloworld")
Output: ("hell", "world", "wor", "ellow")
Example 3
Input: @words = ("a", "aa", "aaa", "aaaa")
Output: ("a", "aa", "aaa")
Example 4
Input: @words = ("flower", "flow", "flight", "fl", "fli", "ig", "ght")
Output: ("flow", "fl", "fli", "ig", "ght")
Example 5
Input: @words = ("car", "carpet", "carpenter", "pet", "enter", "pen", "pent")
Output: ("car", "pet", "enter", "pen", "pent")
Solution
Perl
For each word, we count the the number of words the current word is a substring of. As a word is a substring of itself, this count is too high by one. Therefore, we select every word that is a substring of at least two words from the list and deduplicate.
use strict;
use warnings;
use List::Util 'uniqstr';
use experimental qw(signatures refaliasing);
sub match_string (@words) {
uniqstr grep {
\my $word = \$_;
1 < grep {
0 <= index($_, $word)
} @words
} @words;
}
See the full solution to task 1.
J
The logic in J is basically the same.
Dissecting the solution:
MatchString =: {{ ~. y #~ 1 < +/"1 +./@E.&>/~ y }}
NB. HH GG FFF EEEE DDD CC BAA
A apply left operation (B-D) to all word pairs
B open word boxes
C identify positions where left word starts as substring in right word
D logical or: Is left word substring of the right word?
E count number of words that the left word is substring of
F \(\gt 1\) other words found? (ignore self-matching)
G use result as selector into the word list
H deduplicate
Transformed into a variable-free, tacit verb:
MatchString =: ~.@(#~ 1&<@(+/"1)@(+./@E.&>/)~)
echo MatchString 'cat'; 'cats'; 'dog'; 'dogcat'; 'dogcat'; 'rat'; 'ratcatdogcat'
The J IDE comes with a powerful interactive tool named dissect to analyze and visualize J sentences.
The verb MatchString applied to example 1 is shown as:
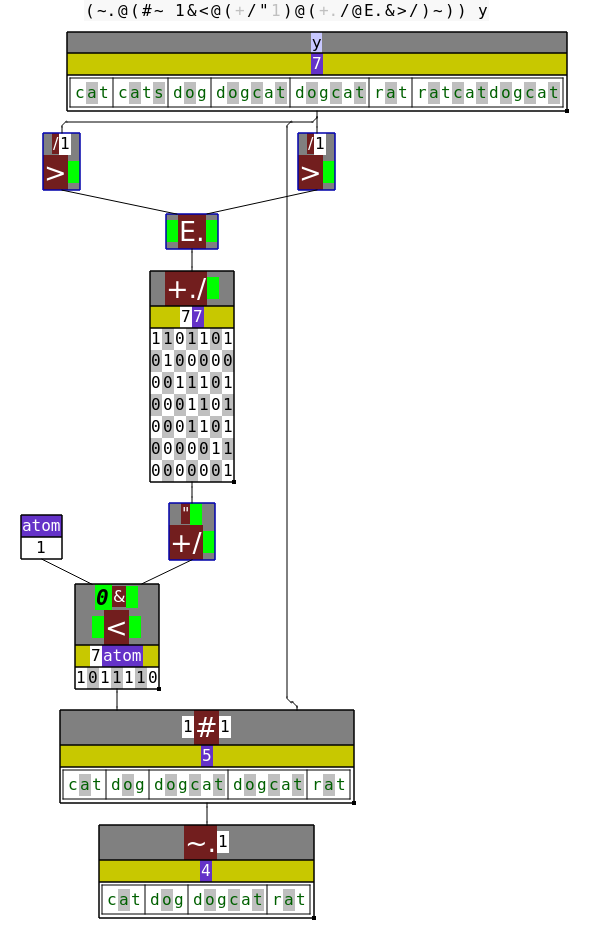
The post’s title references the square matrix that can be seen in the middle of this graph, as well as the triangular shape from task 2.
See the full solution.
Task 2: Binary Prefix
Submitted by: Mohammad Sajid Anwar
You are given an array, @nums, where each element is either 0 or 1.
Define \(x_i\) as the number formed by taking the first \(i+1\) bits of @nums (from $nums[0] to $nums[i]) and interpreting them as a binary number, with $nums[0] being the most significant bit.
For example:
If @nums = (1, 0, 1), then:
x0 = 1 (binary 1)
x1 = 2 (binary 10)
x2 = 5 (binary 101)
For each \(i\), check whether \(x_i\) is divisible by 5.
Write a script to return an array @answer where $answer[i] is true if \(x_i\) is divisible by 5, otherwise false.
Example 1
Input: @nums = (0,1,1,0,0,1,0,1,1,1)
Output: (true, false, false, false, false, true, true, false, false, false)
Binary numbers formed (decimal values):
0: 0
01: 1
011: 3
0110: 6
01100: 12
011001: 25
0110010: 50
01100101: 101
011001011: 203
0110010111: 407
Example 2
Input: @num = (1,0,1,0,1,0)
Output: (false, false, true, true, false, false)
1: 1
10: 2
101: 5
1010: 10
10101: 21
101010: 42
Example 3
Input: @num = (0,0,1,0,1)
Output: (true, true, false, false, true)
0: 0
00: 0
001: 1
0010: 2
00101: 5
Example 4
Input: @num = (1,1,1,1,1)
Output: (false, false, false, true, false)
1: 1
11: 3
111: 7
1111: 15
11111: 31
Example 5
Input: @num = (1,0,1,1,0,1,0,0,1,1)
Output: (false, false, true, false, false, true, true, true, false, false)
1: 1
10: 2
101: 5
1011: 11
10110: 22
101101: 45
1011010: 90
10110100: 180
101101001: 361
1011010011: 723
Solution
Perl
The list of intermediate integers is the same as all the intermediate reductions when transforming the whole binary string into an integer via the usual formula \(x_0 = b_0\), \(x_i = 2x_{i-1} + b_i\) using e.g. reduce.
These intermediate results - as provided by reductions - just need to be checked against divisibility by 5.
use strict;
use warnings;
use List::Util 'reductions';
sub binary_prefix {
map 0+!($_ % 5), reductions {2 * $a + $b} @_;
}
See the full solution to task 2.
J
Similarly, a solution in J is straightforward:
BinaryPrefix =: {{ 0 = 5 | #.\ y }}
NB. DDD CCC BBA
A generate all prefixes from the binary list and apply the left operation (B) to each of them
B convert binary array to integer value
C find the remainder when dividing by 5
D compare against zero
Again, as a variable-free, tacit verb:
BinaryPrefix =: 0&=@(5&|@#.\)
echo ('false'; 'true') {~ BinaryPrefix 0 1 1 0 0 1 0 1 1 1
See the full solution.