| 02 January 2026 | Challenge 354 |
Shifted Differences
Task 1: Min Abs Diff
Submitted by: Mohammad Sajid Anwar
You are given an array of distinct integers.
Write a script to find all pairs of elements with the minimum absolute difference.
Rules (a,b):
1: a, b are from the given array.
2: a < b
Example 1
Input: @ints= (4, 2, 1, 3)
Output: [1, 2], [2, 3], [3, 4]
Example 2
Input: @ints = (10, 100, 20, 30)
Output: [10, 20], [20, 30]
Example 3
Input: @ints = (-5, -2, 0, 3)
Output: [-2, 0]
Example 4
Input: @ints = (8, 1, 15, 3)
Output: [1, 3]
Example 5
Input: @ints = (12, 5, 9, 1, 15)
Output: [9, 12], [12, 15]
Solution
Perl
Take the difference between all pairs from the list, set non-positive values to BAD, compare the result to the minimum, find the indices of matching elements, select list elements according to the found indices and sort lexicographically.
use strict;
use warnings;
use PDL;
sub min_diff {
my $i = long @_;
my $diff = $i->dummy(0) - $i;
$diff->badflag(1);
$diff->where($diff <= 0) .= $diff->badvalue;
qsortvec $i->index1d(scalar whichND $diff == $diff->min);
}
See the full solution to task 1.
J
The implementation in J follows the same logic.
Differing details:
- non-positive values are set to \(\infty\)
- finding indices in a multi-dimensional array is emulated by indexing the flattened array and transforming back to multi-dimensional indices.
MinDiff =: /:~@({~ ($ #: I.@,)@(= <./@,)@:(_:^:(0&>:)"0)@(-~/~))
echo MinDiff 4 2 1 3
Example 1 dissected:
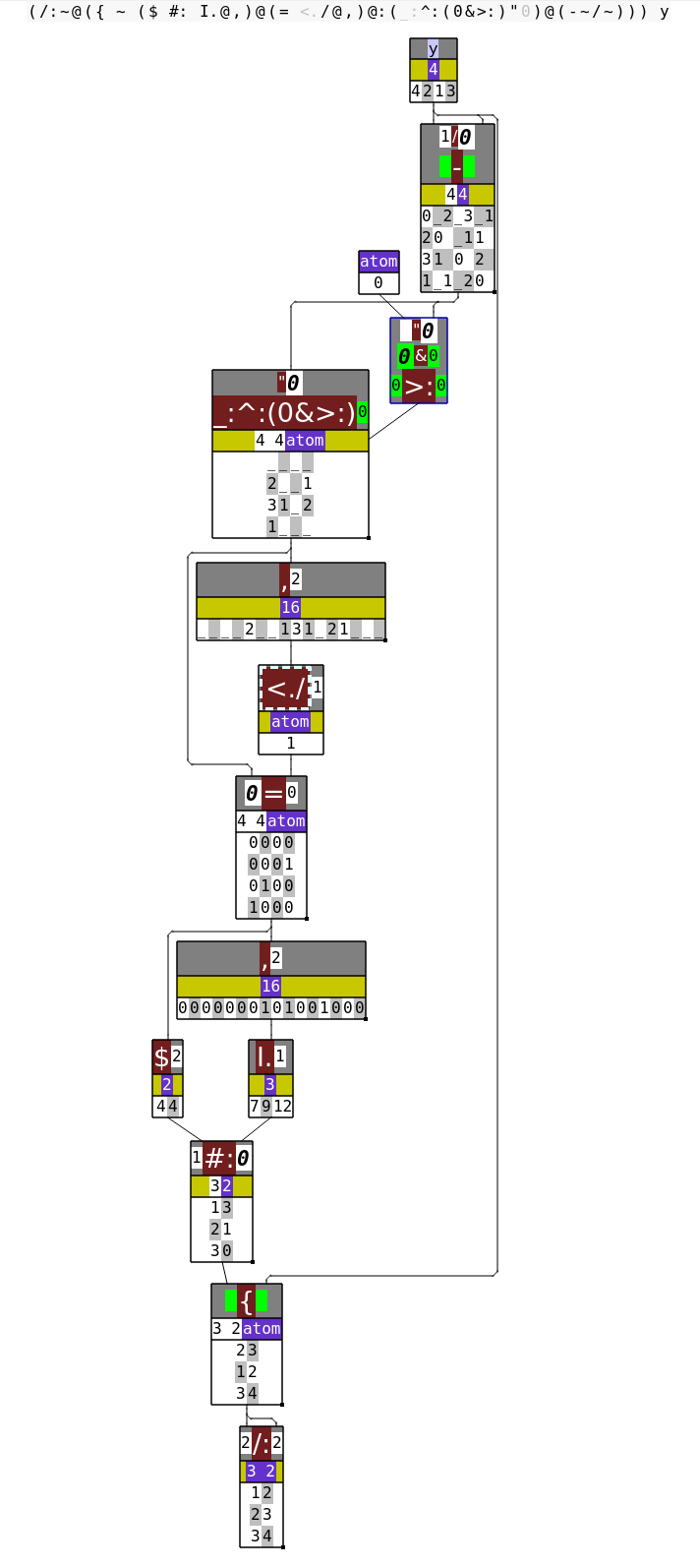See the full solution.
Task 2: Shift Grid
Submitted by: Mohammad Sajid Anwar
You are given m x n matrix and an integer, $k > 0.
Write a script to shift the given matrix $k times.
Each shift follow the rules:
Rule 1:
Element at grid[i][j] moves to grid[i][j + 1]
This means every element moves one step to the right within its row.
Rule 2:
Element at grid[i][n - 1] moves to grid[i + 1][0]
This handles the last column: elements in the last column of row i
wrap to the first column of the next row (i+1).
Rule 3:
Element at grid[m - 1][n - 1] moves to grid[0][0]
Example 1
Input: @matrix = ([1, 2, 3],
[4, 5, 6],
[7, 8, 9],)
$k = 1
Output: ([9, 1, 2],
[3, 4, 5],
[6, 7, 8],)
Rule 1: grid[i][j] -> grid[i][j+1] for j < n-1.
We take elements from the original grid at (i, j) and put them into new_grid[i][j+1].
From original:
(0,0): 1 -> new_grid[0][1] = 1
(0,1): 2 -> new_grid[0][2] = 2
(1,0): 4 -> new_grid[1][1] = 4
(1,1): 5 -> new_grid[1][2] = 5
(2,0): 7 -> new_grid[2][1] = 7
(2,1): 8 -> new_grid[2][2] = 8
New grid looks after Rule 1:
([?, 1, 2],
[?, 4, 5],
[?, 7, 8],)
Rule 2: grid[i][n-1] -> grid[i+1][0] for i < m-1.
Elements from original last column (except last row) go to next row's first column.
From original:
(0,2): 3 -> new_grid[1][0] = 3
(1,2): 6 -> new_grid[2][0] = 6
Now new grid after Rules 1 + 2:
([?, 1, 2],
[3, 4, 5],
[6, 7, 8],)
Rule 3: grid[m-1][n-1] -> grid[0][0].
Original (2,2): 9 -> new_grid[0][0] = 9.
Now new_grid is complete:
([9, 1, 2],
[3, 4, 5],
[6, 7, 8],)
Example 2
Input: @matrix = ([10, 20],
[30, 40],)
$k = 1
Output: ([40, 10],
[20, 30],)
Rule 1 (move right in same row if not last column):
(0,0): 10 -> new[0][1] = 10
(1,0): 30 -> new[1][1] = 30
After Rule 1:
([?, 10],
[?, 30],)
Rule 2 (last col -> next row’s first col, except last row):
(0,1): 20 -> new[1][0] = 20
After Rule 2:
([?, 10],
[20, 30],)
Rule 3 (bottom-right to top-left):
(1,1): 40 -> new[0][0] = 40
After Rule 3:
([40, 10],
[20, 30],)
Example 3
Input: @matrix = ([1, 2],
[3, 4],
[5, 6],)
$k = 1
Output: ([6, 1],
[2, 3],
[4, 5],)
Rule 1:
(0,0): 1 -> new[0][1] = 1
(1,0): 3 -> new[1][1] = 3
(2,0): 5 -> new[2][1] = 5
After Rule 1:
( [?, 1],
[?, 3],
[?, 5],)
Rule 2:
(0,1): 2 -> new[1][0] = 2
(1,1): 4 -> new[2][0] = 4
After Rule 2:
([?, 1],
[2, 3],
[4, 5],)
Rule 3:
(2,1): 6 -> new[0][0] = 6
After Rule 3:
([6, 1],
[2, 3],
[4, 5],)
Example 4
Input: @matrix = ([1, 2, 3],
[4, 5, 6],)
$k = 5
Output: ([2, 3, 4],
[5, 6, 1],)
Shift 1
Rule 1
1 -> (0,1)
2 -> (0,2)
4 -> (1,1)
5 -> (1,2)
Rule 2
3 -> (1,0) (last column of row 0)
Rule 3
6 -> (0,0) (bottom-right corner)
Result
[6, 1, 2]
[3, 4, 5]
----------------------------
Shift 2
Starting from the previous matrix:
[6, 1, 2]
[3, 4, 5]
Rule 1
6 -> (0,1)
1 -> (0,2)
3 -> (1,1)
4 -> (1,2)
Rule 2
2 -> (1,0)
Rule 3
5 -> (0,0)
Result
[5, 6, 1]
[2, 3, 4]
----------------------------
Shift 3
[5, 6, 1]
[2, 3, 4]
Rule 2: 1 -> (1,0)
Rule 3: 4 -> (0,0)
Others follow Rule 1
Result
[4, 5, 6]
[1, 2, 3]
----------------------------
Shift 4
[4, 5, 6]
[1, 2, 3]
Result
[3, 4, 5]
[6, 1, 2]
----------------------------
Shift 5
[3, 4, 5]
[6, 1, 2]
Result
[2, 3, 4]
[5, 6, 1]
Final Output (after k = 5 shifts)
([2, 3, 4],
[5, 6, 1])
Example 5
Input: @matrix = ([1, 2, 3, 4])
$k = 1
Output: ([4, 1, 2, 3])
Rule 1:
(0,0): 1 -> new[0][1] = 1
(0,1): 2 -> new[0][2] = 2
(0,2): 3 -> new[0][3] = 3
After Rule 1:
([?, 1, 2, 3])
Rule 2:
(0,3): 4 -> new[1][0] ??
Wait — but i=0, n-1=3, next row i+1=1 doesn’t exist (m=1).
So this is actually a special case where Rule 2 should not apply.
because m=1, so (0,3) goes by Rule 3 actually.
The rules say:
grid[i][j] -> grid[i][j+1] for j < n-1.
grid[i][n-1] -> grid[i+1][0] for i < m-1.
grid[m-1][n-1] -> grid[0][0].
For m = 1:
Elements (0,0),(0,1),(0,2) follow Rule 1 -> (0,1),(0,2),(0,3).
Element (0,3) is (m-1, n-1), so follows Rule 3 -> (0,0).
Actually, that means after Rule 1:
We put 1,2,3 in positions 1,2,3, leaving position 0 empty.
Then Rule 3 puts 4 in position 0.
So final directly:
[4, 1, 2, 3]
Solution
The rules can easily be implemented by flattening the matrix, rotating the resulting list rightwards and re-arrange the list to its original shape.
Perl
use strict;
use warnings;
use PDL;
sub shift_grid ($k, @m) {
my $grid = long @m;
$grid->flat->rotate($k)->reshape($grid->dims);
}
See the full solution to task 2.
J
ShiftGrid =: $@] $ -@[ |. ,@]
echo 1 ShiftGrid (1 2 3), (4 5 6),: 7 8 9
Example 1 dissected:
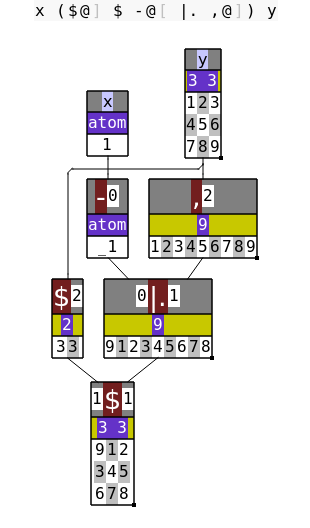
See the full solution.