09 January 2026

Challenge 355

Separated Mountains

• Task 1: Thousand Separator
• Task 2: Mountain Array

Task 1: Thousand Separator

Submitted by: Mohammad Sajid Anwar

---

You are given a positive integer, $int.

Write a script to add thousand separator, , and return as string.

Example 1

Input: $int = 123
Output: "123"

Example 2

Input: $int = 1234
Output: "1,234"

Example 3

Input: $int = 1000000
Output: "1,000,000"

Example 4

Input: $int = 1
Output: "1"

Example 5

Input: $int = 12345
Output: "12,345"

---

Solution

When I read this task I instantly remembered my weird solution to task 1 from week 322. The lesson I learned was: If some kind of remainder shall be placed at the head of an otherwise equally parted result, processing the reversed list or string may lead to a simpler solution. Following that approach.

Perl

Another detail I remember from week 322 was a solution based on unpack. So here is my approach:

use strict;
use warnings;

sub tsep {
    scalar reverse join ',', unpack "(a3)*", scalar reverse shift;
}

See the full solution to task 1.

J

One of J’s nice features is the Under (Dual) conjunction &. that transforms the cells of an array with one given verb, applies a second verb to the transformed cells and then inverts the first transformation. Here the transformation is “reverse” (which is its own inverse).

tsep =: ;@((, (<',')&,)/)@(_3&(<\))&.|.@":
NB.     H   GGGGGGGGGG F   EE  DC  BBBB AA

echo tsep 12345

A: convert number to character array
B: apply left verb (C-H) on the reversed array, then (un)reverse
C: apply left verb (D) to chunks of the right argument in the size given by E
D: box a chunk
E: non-overlapping chunks of 3 elements (at most)
F: insert left verb (G) between all pairs of consecutive elements
G: join the left and the right (boxed) element with a boxed comma
H: remove one level of boxing

Dissecting example 5:

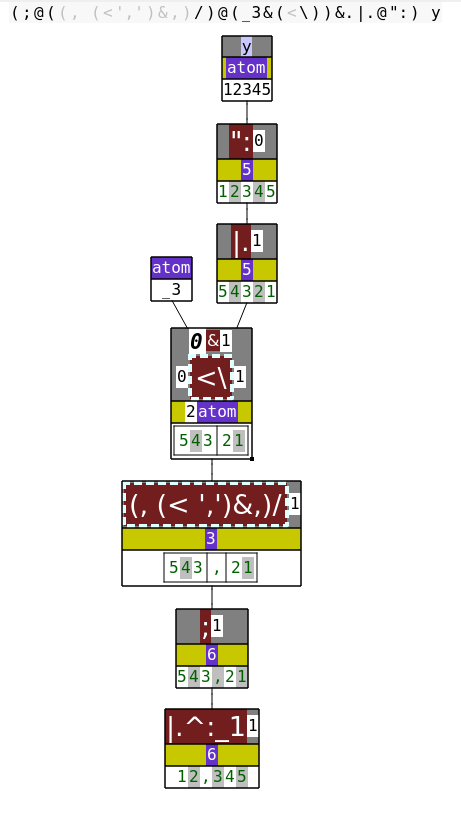
See the full solution.

Task 2: Mountain Array

Submitted by: Mohammad Sajid Anwar

---

You are given an array of integers, @ints.

Write a script to return true if the given array is a valid mountain array.

An array is mountain if and only if:
1) arr.length >= 3
and
2) There exists some i with 0 < i < arr.length - 1 such that:
arr[0] < arr[1]     < ... < arr[i - 1] < arr[i]
arr[i] > arr[i + 1] > ... > arr[arr.length - 1]

Example 1

Input: @ints = (1, 2, 3, 4, 5)
Output: false

Example 2

Input: @ints = (0, 2, 4, 6, 4, 2, 0)
Output: true

Example 3

Input: @ints = (5, 4, 3, 2, 1)
Output: false

Example 4

Input: @ints = (1, 3, 5, 5, 4, 2)
Output: false

Example 5

Input: @ints = (1, 3, 2)
Output: true

---

Solution

Given the numbers \((x_1,\ldots,x_n)\) we define steps \(s_i\) as:

\[s_i = \operatorname{sign}(x_{i+1} - x_i)\]

and consider consecutive step pairs \(q_i\):

\[q_i = (s_i, s_{i+1})\]

There are only three valid step pairs \(p_k\):

\[\begin{align*} p_1 &= (1, -1)\\ p_2 &= (1, 1)\\ p_3 &= (-1, -1) \end{align*}\]

corresponding to a peak, an ascending or a descending triplet of numbers.

Comparing \(q_i\) with \(p_k\) produces a binary indicator matrix \(v_{ik}\):

\[v_{ik} = \begin{cases} 1&\text{if $q_i = p_k$}\\ 0&\text{otherwise} \end{cases}\]

For a mountain array, obviously all step pairs need to be valid. In terms of the indicator matrix this may be expressed as:

\[v = \bigwedge_{i=1}^{n-2} \bigvee_{k=1}^3 v_{ik}\]

As it is not possible to come from a descending to an ascending sequence via valid step pairs, the only remaining condition is the existence of at least one peak triplet, which may be expressed in terms of the indicator matrix as:

\[\hat{v} = \bigvee_{i=1}^{n-2} v_{i0}\]

The final result may then expressed as:

\[v \wedge \hat{v}\]

Though these steps may look complicated, they are simple and basic in languages providing vectorized operations, such as PDL or J.

Perl

• Calculating \(s_i\) as ...->diff2 <=> 0 follows exactly the above definition
• \(q_i\) as ...->lags(0, 1, 2)->xchg(0, 1)->(-1:0) is a bit trickier
• \(v_{ik}\) can be constructed with eqvec with suitable dimensions of its operands
• the final calculations on \(v_{ik}\) are straightforward

use strict;
use warinings;
use PDL;
use PDL::NiceSlice;

sub mountain {
    state $p = long '1 -1; 1 1; -1 -1';
    my $v = eqvec +(long(@_)->diff2 <=> 0)
        ->lags(0, 1, 2)->xchg(0, 1)->(-1:0)->dummy(1), $p;

    $v->orover->andover && $v((0))->orover;
}

See the full solution to task 2.

J

The logic is almost identical, though J has a different set of primitive operations to accomplish the result.

p =. 1 _1; 1 1; _1 _1
Mountain =: (+./@{. *. *./@(+./))@(p&(e."(1 0)~))@(2&(<\))@:*@(2&(-~/\))
NB.          NNN MM LL KKK  III    HHHHHHHHHHHHH   G  FE    D  C  BBBA

echo Mountain 0 2 4 6 4 2 0

A: apply left verb (B) on chunks in the size given by C
B: take the difference between swapped elements
C: sliding (overlapping) chunks of 2 elements
D: sign, A-D produce \(s_i\)
E: apply left verb (F) on chunks in the size given by G
F: box each chunk
G: sliding (overlapping) chunks of 2 elements, E-G produce \(q_i\)
H: check validity of each step pair, H produces \(v_{ik}\)
I: logical or over columns
K: logical and over elements, I,K produce \(v\)
L: logical and between I,K and M,N: the final result \(v \wedge \hat{v}\)
M: first row
N: logical or over elements, M,N produce \(\hat{v}\)

Dissecting the non-mountain array 1 3 5 7 4 2 2:

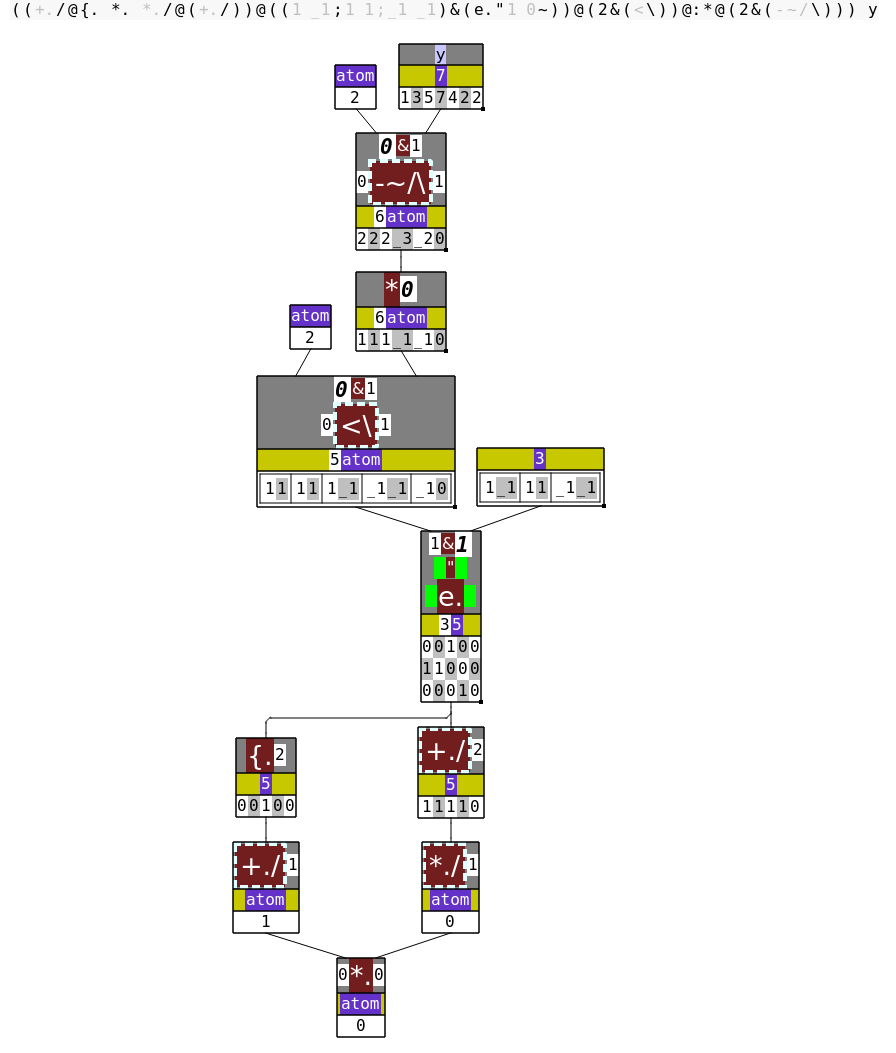
See the full solution.